“机器学习”系列之Perceptron（感知机）-人工智能-PHP中文网

“机器学习”系列之Perceptron（感知机）

P粉084495128

发布： 2025-08-01 09:52:59

原创

263人浏览过

感知机是二分类的线性分类模型，输入为实例的特征向量，输出为实例的类别（取+1和-1）。感知机对应于输入空间中将实例划分为两类的分离超平面。感知机旨在求出该超平面，为求得超平面导入了基于误分类的损失函数，利用梯度下降法对损失函数进行最优化。

☞☞☞AI 智能聊天, 问答助手, AI 智能搜索, 免费无限量使用 DeepSeek R1 模型☜☜☜

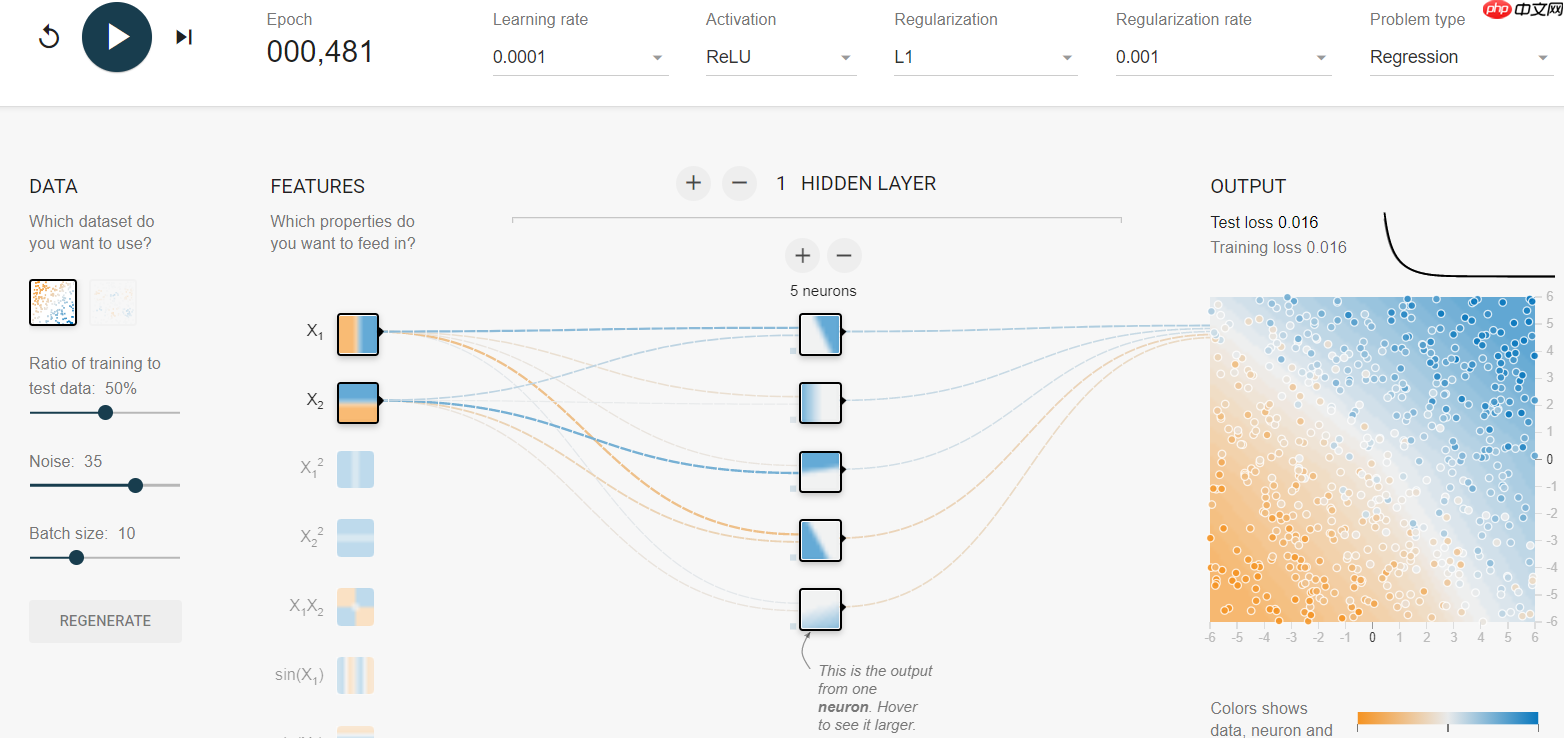
“机器学习”系列之perceptron（感知机） - php中文网

“机器学习”系列之感知机

0 简介

感知机是二分类的线性分类模型，输入为实例的特征向量，输出为实例的类别（取+1和-1）。感知机对应于输入空间中将实例划分为两类的分离超平面。感知机旨在求出该超平面，为求得超平面导入了基于误分类的损失函数，利用梯度下降法对损失函数进行最优化。

同时介绍一个可视化实验网址，效果如下：网站链接

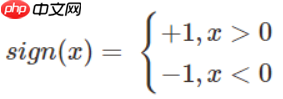
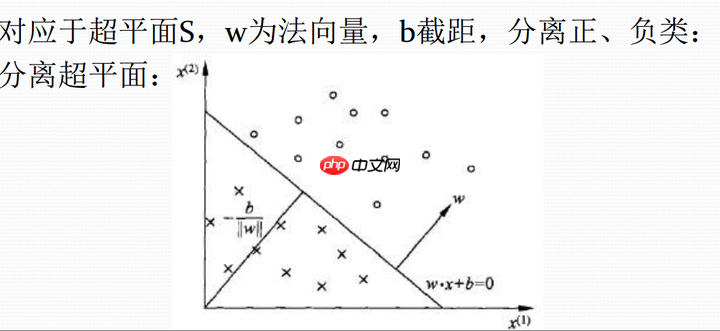
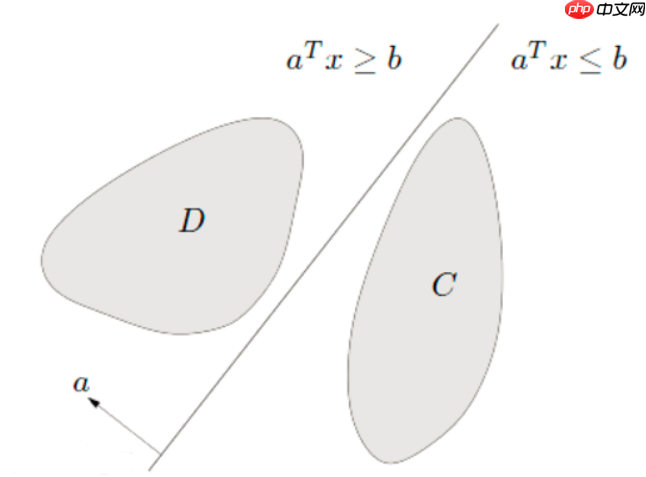
“机器学习”系列之Perceptron（感知机） - php中文网

1 感知机模型

假设输入空间（特征向量）是 $x \in R^{n}$ x∈Rn，输出空间为,输入 $Y \in - 1, 1$ Y∈−1,1表示实例的特征向量，对应于输入空间的点，输出 $x \in X$ x∈X表示实例的类别，则由输入空间到输出空间的表达形式为：

“机器学习”系列之Perceptron（感知机） - php中文网

上面该函数称为感知机，其中w，b称为模型的参数， $x \in R^{n}$ x∈Rn称为权值， $b$ b称为偏置， $w * x$ w∗x表示为 $w ， x$ w，x的内积

“机器学习”系列之Perceptron（感知机） - php中文网

如果我们将sign称之为激活函数的话，感知机与logistic regression的差别就是感知机激活函数是sign，logistic regression的激活函数是sigmoid。sign(x)将大于0的分为1，小于0的分为-1；sigmoid将大于0.5的分为1，小于0.5的分为0。因此sign又被称为单位阶跃函数，logistic regression也被看作是一种概率估计。
该感知机线性方程表示为： $w * x + b = 0$ w∗x+b=0，它的几何意义如下图所示：

“机器学习”系列之Perceptron（感知机） - php中文网

学习参数w与b，确定了w与b，图上的直线（高维空间下为超平面）也就确定了，那么以后来一个数据点，我用训练好的模型进行预测判断，如果大于0就分类到+1，如果小于0就分类到-1。
用到了超平面分离定理：超平面分离定理是应用凸集到最优化理论中的重要结果，这个结果在最优化理论中有重要的位置。所谓两个凸集分离，直观地看是指两个凸集合没有交叉和重合的部分，因此可以用一张超平面将两者隔在两边。如下图所示，在大于0的时候，我将数据点分类成了D类，在小于0的时候，我将数据点分类成了C类

“机器学习”系列之Perceptron（感知机） - php中文网

Giiso写作机器人

Giiso写作机器人，让写作更简单

查看详情

2 感知机学习策略

学习出超平面的参数w，b，这就需要用到我们的学习策略。距离公式如下:

$\frac{1}{∣ w ∣} ∣ w * x_{0} + b ∣$ ∣w∣1∣w∗x0+b∣

每一个误分类点都满足: $- y_{i} (w * x_{0} + b) > 0$ −yi(w∗x0+b)>0
因为当我们数据点正确值为+1的时候，你误分类了，那么你判断为-1，则算出来 $(w * x_{0} + b) < 0$ (w∗x0+b)<0,所以满足 $- y_{i} (w * x_{0} + b) > 0$ −yi(w∗x0+b)>0
当数据点是正确值为-1的时候，你误分类了，那么你判断为+1，则算出来 $(w * x_{0} + b) > 0$ (w∗x0+b)>0,所以满足 $- y_{i} (w * x_{0} + b) > 0$ −yi(w∗x0+b)>0
得到误分类点的距离为：

$- \frac{1}{∣ w ∣} y_{i} (w * x_{i} + b)$ −∣w∣1yi(w∗xi+b)

又因 $- y_{i} (w * x_{0} + b) > 0$ −yi(w∗x0+b)>0,所以可以直接将绝对值去掉。那么可以得到总距离为：

$- \frac{1}{∣ w ∣} Σ y_{i} (w * x_{i} + b)$ −∣w∣1Σyi(w∗xi+b)

不考虑 $\frac{1}{∣ w ∣}$ ∣w∣1，我们可以得到损失函数为：

$L (w, b) = - Σ y_{i} (w * x_{i} + b)$ L(w,b)=−Σyi(w∗xi+b)

其中M为误分类点的数目。

3 总结

感知机的模型是 $f (x) = s i g n (w * x + b)$ f(x)=sign(w∗x+b)，它的任务是解决二分类问题，要得到感知机模型我们就需要学习到参数w，b。
学习策略，不断的迭代更新w，b，所以我们需要找到一个损失函数。很自然的我们想到用误分类点的数目来表示损失函数，但是由于不可导，无法进行更新，改为误分类点到超平面的距离来表示，然后不考虑 $\frac{1}{∣ w ∣}$ ∣w∣1，得到我们最终的损失函数

4 代码实现

以iris数据集中两个分类的数据和[sepal length，sepal width]作为特征进行代码举例

4.1 导包、数据集加载

In [1]

import pandas as pdimport numpy as npfrom sklearn.datasets import load_irisimport matplotlib.pyplot as plt
%matplotlib inline

登录后复制

In [2]

# load datairis = load_iris()
df = pd.DataFrame(iris.data, columns=iris.feature_names)
df['label'] = iris.target

登录后复制

In [3]

#df.columns = ['sepal length', 'sepal width', 'petal length', 'petal width', 'label']
df.label.value_counts()

登录后复制

2    50
1    50
0    50
Name: label, dtype: int64

登录后复制

In [4]

plt.scatter(df[:50]['sepal length'], df[:50]['sepal width'], label='0')
plt.scatter(df[50:100]['sepal length'], df[50:100]['sepal width'], label='1')
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.legend()

登录后复制

<matplotlib.legend.Legend at 0x7f70182f1490>

登录后复制

<Figure size 432x288 with 1 Axes>

登录后复制

In [5]

data = np.array(df.iloc[:100, [0, 1, -1]])

登录后复制

In [6]

X, y = data[:,:-1], data[:,-1]

登录后复制

In [7]

y = np.array([1 if i == 1 else -1 for i in y])

登录后复制

4.2 定义Perceptron（感知机）函数

In [9]

# 数据线性可分，二分类数据# 此处为一元一次线性方程class Model:
    def __init__(self):
        self.w = np.ones(len(data[0])-1, dtype=np.float32)
        self.b = 0
        self.l_rate = 0.1
        # self.data = data
    
    def sign(self, x, w, b):
        y = np.dot(x, w) + b        return y    
    # 随机梯度下降法
    def fit(self, X_train, y_train):
        is_wrong = False
        while not is_wrong:
            wrong_count = 0
            for d in range(len(X_train)):
                X = X_train[d]
                y = y_train[d]                if y * self.sign(X, self.w, self.b) <= 0:
                    self.w = self.w + self.l_rate*np.dot(y, X)
                    self.b = self.b + self.l_rate*y
                    wrong_count += 1
            if wrong_count == 0:
                is_wrong = True
        return 'Perceptron Model!'
        
    def score(self):
        pass

登录后复制

In [10]

perceptron = Model()
perceptron.fit(X, y)

登录后复制

'Perceptron Model!'

登录后复制

4.3 结果展示

In [11]

x_points = np.linspace(4, 7,10)
y_ = -(perceptron.w[0]*x_points + perceptron.b)/perceptron.w[1]
plt.plot(x_points, y_)

plt.plot(data[:50, 0], data[:50, 1], 'bo', color='blue', label='0')
plt.plot(data[50:100, 0], data[50:100, 1], 'bo', color='orange', label='1')
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.legend()

登录后复制

<matplotlib.legend.Legend at 0x7f7f43472150>

登录后复制

<Figure size 432x288 with 1 Axes>

登录后复制

4.4 使用scikit-learn中的Perceptron方法

In [15]

from sklearn.linear_model import Perceptron

登录后复制

In [27]

clf = Perceptron(fit_intercept=False,max_iter=5000, shuffle=False)
clf.fit(X, y)

登录后复制

Perceptron(alpha=0.0001, class_weight=None, early_stopping=False, eta0=1.0,
           fit_intercept=False, max_iter=5000, n_iter_no_change=5, n_jobs=None,
           penalty=None, random_state=0, shuffle=False, tol=0.001,
           validation_fraction=0.1, verbose=0, warm_start=False)

登录后复制

In [28]

# Weights assigned to the features.print(clf.coef_)

登录后复制

[[ 16.3 -24.2]]

登录后复制

In [29]

# 截距 Constants in decision function.print(clf.intercept_)

登录后复制

[0.]

登录后复制

In [30]

x_ponits = np.arange(4, 8)
y_ = -(clf.coef_[0][0]*x_ponits + clf.intercept_)/clf.coef_[0][1]
plt.plot(x_ponits, y_)

plt.plot(data[:50, 0], data[:50, 1], 'bo', color='blue', label='0')
plt.plot(data[50:100, 0], data[50:100, 1], 'bo', color='orange', label='1')
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.legend()

登录后复制

<matplotlib.legend.Legend at 0x7f7ef401f410>

登录后复制

<Figure size 432x288 with 1 Axes>

登录后复制

以上就是“机器学习”系列之Perceptron（感知机）的详细内容，更多请关注php中文网其它相关文章！

大家都在看：

即梦AI官方正版免费体验入口即梦AI网页版免安装使用有道智云AI分析在线入口有道智云人工智能免费分析使用入口豆包AI搜索助手入口豆包AI智能检索免费网页版一键部署AI视频生成 | 本地部署AI视频软件教程秘塔AI语音入口在哪里 AI语音互动入口秘塔直达链接