满射、单射与双射：它们之间有何区别与联系？-电脑知识-PHP中文网

单射要求不同输入对应不同输出，满射要求值域全覆盖，双射则是单射与满射的结合，实现一一对应。

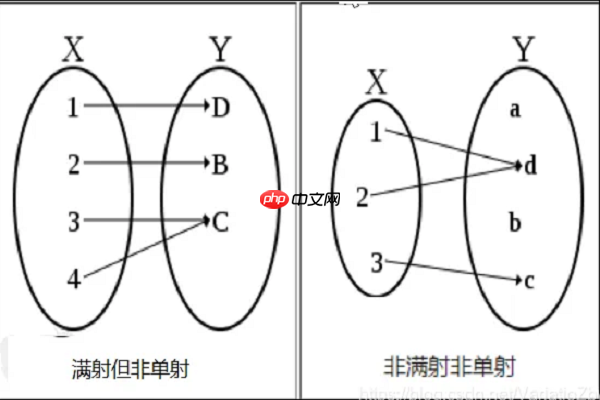
满射、单射与双射：它们之间有何区别与联系？

满射、单射和双射，这些概念其实是函数在映射关系上表现出的不同“性格”。说白了，它们描述的是一个函数如何把定义域里的元素“派发”到值域里去，以及值域里的元素是如何被“接收”的。

单射（Injection/One-to-one）强调的是“不重复”，即不同的输入一定对应不同的输出。
满射（Surjection/Onto）强调的是“全覆盖”，即值域中的每一个元素都能找到至少一个对应的输入。
双射（Bijection/One-to-one correspondence）则是前两者的结合，它既不重复又全覆盖，意味着输入和输出之间存在一种完美的、一一对应的关系，没有任何遗漏或冗余。

解决方案

要深入理解满射、单射与双射，我们不妨从它们各自的定义和直观感受入手，再看看它们是如何相互关联的。

单射（Injection） 一个函数 $f: X \to Y$ 被称为单射，如果对于 $X$ 中任意两个不同的元素 $x_1$ 和 $x_2$，它们在 $Y$ 中的像 $f(x_1)$ 和 $f(x_2)$ 也不同。用数学语言表达就是：如果 $f(x_1) = f(x_2)$，则必然有 $x_1 = x_2$。

直观理解：你可以想象成每个人（输入）都有一个独特的座位（输出），而且没有两个不同的人坐同一个座位。每个座位最多只能被一个人占据。
例子：
1. 函数 $f(x) = x + 1$，定义域和值域都是实数集 $\mathbb{R}$。如果你取两个不同的 $x_1$ 和 $x_2$，那么 $x_1+1$ 和 $x_2+1$ 也必然不同。
2. 身份识别系统中的用户ID生成，通常要求是单射的，以保证每个用户都有唯一的标识。

满射（Surjection） 一个函数 $f: X \to Y$ 被称为满射，如果 $Y$ 中的每一个元素 $y$ 都在 $X$ 中至少有一个原像 $x$，使得 $f(x) = y$。换句话说，函数的值域（Range）与它的上域（Codomain）完全相等。

直观理解：这就像是所有的座位（值域）都被人（输入）坐满了，没有一个座位是空着的。每个座位至少被一个人占据。
例子：
1. 函数 $f(x) = x^3$，定义域和值域都是实数集 $\mathbb{R}$。对于任何实数 $y$，你总能找到一个实数 $x = \sqrt[3]{y}$ 使得 $f(x) = y$。
2. 一个资源调度系统，如果能确保所有可用的计算节点（值域）都能接收到任务（输入），那么这个调度函数就是满射的。

双射（Bijection） 一个函数 $f: X \to Y$ 被称为双射，如果它既是单射又是满射。

直观理解：每个人都有一个独特的座位，并且所有的座位都被坐满了。这意味着输入和输出之间建立了一种完美的一一对应关系。每个座位恰好被一个人占据，没有空座，也没有人抢座。
例子：
1. 函数 $f(x) = x$，定义域和值域都是实数集 $\mathbb{R}$。它显然是单射（不同 $x$ 对应不同 $x$）和满射（任何 $y$ 都能找到 $x=y$）。
2. 加密和解密过程，一个好的对称加密算法，加密函数通常是双射的，这样才能保证密文可以无损地解密回原文。

区别与联系

区别：
- 单射关注的是“一对一或多对一”，但绝不能“一对多”（这不是函数）。它强调输出的唯一性。
- 满射关注的是“覆盖性”，即值域中的每个元素都被“触及”了。
- 双射则兼顾了这两点。
联系：
- 双射是最强的性质，它蕴含了单射和满射。
- 如果一个函数是双射，那么它一定存在一个逆函数，这个逆函数也是双射。这是双射函数一个非常重要的特性。
- 在有限集之间，如果存在一个双射，那么这两个集合的元素个数是相等的。这是数学中定义集合“大小”的基础。

如何在编程和数学建模中判断函数是单射、满射还是双射？

在我看来，判断一个函数属于哪种类型，这不只是理论上的推导，更多时候是结合实际场景和数据特性来选择合适的判断方法。

判断单射（Injection）

理论方法：假设 $f(x_1) = f(x_2)$，然后通过代数推导，如果能得出 $x_1 = x_2$，那么这个函数就是单射。
编程实践：
- 离散数据：如果你处理的是有限的、离散的输入和输出，比如一个将用户ID映射到内部索引的函数。你可以用一个哈希表（或 Set）来存储所有已生成的输出值。每次生成新值时，检查这个值是否已存在于哈希表中。如果存在，那么这个函数就不是单射的（发生了碰撞）。
- 连续函数：对于像 $f(x) = x^2$ 这样的函数，在实数域上它就不是单射的，因为 $f(-1) = f(1) = 1$。如果函数是可导的，可以考察其导数。如果导数在定义域内始终为正或始终为负（即函数是严格单调的），那么它是单射。不过，这只是充分条件，不是必要条件。图形法也是一种直观方式，如果任何水平线与函数图像最多只有一个交点，那就是单射。
个人观点：在系统设计中，比如生成唯一标识符（GUID、数据库主键），我们天然就希望它是一个单射的映射，确保数据的唯一性和完整性。如果不是，那就会导致数据冲突，非常麻烦。

判断满射（Surjection）

理论方法：对于值域 $Y$ 中的任意一个元素 $y$，尝试找到一个 $X$ 中的元素 $x$，使得 $f(x) = y$。这通常需要解一个方程 $y = f(x)$。
编程实践：
- 离散数据：如果你知道值域 $Y$ 的所有可能元素，你可以遍历 $Y$ 中的每个元素，并尝试找到一个 $X$ 中的元素能够映射到它。或者，你可以计算出函数的所有可能输出，然后检查这些输出是否覆盖了整个值域。
- 连续函数：这通常涉及分析函数的范围。例如，$f(x) = x^2$ 从 $\mathbb{R}$ 到 $\mathbb{R}$ 就不是满射的，因为它的值域是 $[0, \infty)$，无法覆盖负实数。但如果将值域限制为 $[0, \infty)$，那么它就是满射的。这需要你了解函数的最大值、最小值、渐近线以及连续性等性质。
个人观点：在一些资源分配或负载均衡的场景中，我们希望所有的资源（目标）都能被充分利用，不留死角。这就要求我们的分配策略是满射的。如果不是，就意味着有资源被闲置，或者有任务无法被处理。

判断双射（Bijection）

理论方法：同时证明函数是单射和满射。
编程实践：
- 存在逆函数：如果一个函数是双射的，那么它一定存在逆函数 $f^{-1}: Y \to X$，并且 $f(f^{-1}(y)) = y$ 且 $f^{-1}(f(x)) = x$。在编程中，如果你能成功实现一个逆操作，并且这个逆操作本身也是一个函数（即满足函数的定义），那么原函数很可能是双射的。
- 计数：对于有限集，如果定义域和值域的元素数量相等，并且函数是单射的，那么它必然是双射的（反之亦然，如果是满射且数量相等，也必然是双射）。
个人观点：加密、压缩、序列化这些操作，核心需求就是可逆性和无损性。一个双射的映射是实现这些目标的关键。如果一个加密算法不是双射，那么解密就可能出现问题，甚至无法还原原始数据，这是灾难性的。

单射、满射与双射在数据结构、算法设计中有哪些具体应用场景？

这些抽象的数学概念，在我们的日常编程和算法设计中，其实无处不在，只是我们可能没有刻意用“单射”、“满射”这样的词去描述它们。

美间AI

美间AI：让设计更简单

查看详情

单射（Injection）的应用

哈希函数（Hash Functions）：理想的哈希函数应该尽可能地接近单射，以减少哈希冲突。虽然完全的单射哈希函数（完美哈希）在实践中很难实现，但我们总是在努力设计能够最大程度减少碰撞的哈希算法，以提高哈希表的性能。
唯一标识符（Unique Identifiers）：数据库的主键、全局唯一标识符（GUID/UUID）、对象ID等，都要求是单射的。每个实体都必须有唯一的标识，否则系统会崩溃或数据会混乱。
映射（Map/Dictionary）的键：在Python的字典、Java的HashMap、C++的std::map等数据结构中，键（Key）到值（Value）的映射就是单射的。每个键都唯一对应一个值，你不能有两个相同的键。
图论中的路径：在一些路径查找算法中，如果要求路径不能重复访问同一个节点，那么从起点到某个节点的映射可以看作是一种单射。

满射（Surjection）的应用

负载均衡（Load Balancing）：一个负载均衡器将请求分发到一组服务器。如果所有的服务器（值域）都能接收到请求（输入），那么这个分发策略就是满射的。这确保了所有可用资源都被利用，避免了某些服务器过载而另一些空闲。
资源池管理：比如线程池、连接池。如果所有的线程或连接（值域）都能被任务（输入）使用到，那么资源分配函数就是满射的。
内存分配器：在某些场景下，内存分配器需要确保所有可用的内存块（值域）都能被应用程序请求（输入）并使用。
编码方案：在一些编码或校验码设计中，可能需要确保所有的输出码字（值域）都能被某些输入数据（输入）所生成，这对于错误检测和纠正很重要。

双射（Bijection）的应用

加密与解密（Encryption and Decryption）：对称加密算法（如AES）就是典型的双射应用。加密函数将明文映射到密文，解密函数则将密文映射回明文。这种映射必须是双射的，才能保证信息的可逆性和无损性。
数据压缩与解压缩（Compression and Decompression）：无损压缩算法（如ZIP）也是双射的。压缩过程将原始数据映射为更小的压缩数据，解压缩则能完整地还原原始数据。
序列化与反序列化（Serialization and Deserialization）：将一个对象转换为字节流（序列化）和将字节流还原为对象（反序列化）的过程，通常也要求是双射的，以确保数据在传输或存储后能够完整地恢复。
哈希表的完美哈希：在某些特殊场景下，如果能构建一个从键到数组索引的完美哈希函数，它就是双射的，每个键都映射到一个唯一的数组索引，且没有冲突，性能极高。
数据结构中的索引：数组的索引与元素之间的关系，在给定数组长度的情况下，可以看作是一种双射。每个索引唯一对应一个元素，反之亦然。

理解这些函数特性对优化算法性能和避免常见错误有何帮助？

在我多年的开发经验中，对函数这些基本特性的理解，常常能帮助我从底层逻辑上优化系统，并规避很多潜在的问题。它就像一个思维框架，让我在设计时能更清晰地看到问题的本质。

优化算法性能

减少冲突与提高效率：
- 单射性：在设计哈希表时，我们追求的“低冲突率”本质上就是对哈希函数单射性的追求。冲突越少，查找、插入、删除的平均时间复杂度就越接近 O(1)。如果能设计一个接近单射的映射，就能避免因冲突处理而带来的额外计算和内存开销。
- 双射性：如果一个数据转换过程是双射的，那么它的逆过程通常也是高效且确定的。比如，一个好的编解码器，编码和解码过程都是双射的，这意味着数据可以快速且无损地来回转换，无需复杂的搜索或猜测。这在实时通信或大数据处理中至关重要。
资源利用率：
- 满射性：在分布式系统或多线程编程中，如果任务分配策略能保证满射，那么所有可用的计算资源都能被充分利用，避免了资源闲置，从而提高了整体吞吐量。一个不满射的调度器可能会导致某些工作节点一直空闲，而其他节点却过载。

避免常见错误

数据丢失或不完整：
- 如果一个本应是双射的映射（比如序列化），实际却不是，那么在反向操作（反序列化）时就可能丢失信息或无法完整还原数据。这会导致数据损坏，是系统中最致命的错误之一。
- 如果一个任务调度器被设计为满射，但实际上存在某些资源永远无法被分配到任务，那么这些资源就可能成为“死角”，导致系统整体效率下降，甚至出现任务堆积。
数据重复或不唯一：
- 如果一个需要唯一标识的系统（如数据库主键生成）没有保证单射性，就会出现ID冲突。这意味着不同的实体被赋予了相同的标识，导致数据混乱、引用错误，甚至破坏数据一致性。
- 在缓存系统中，如果键到值的映射不是单射的，不同的键可能意外地映射到相同的值，或者相同的键在不同时间映射到不同的值，导致缓存失效或数据不一致。
不可逆操作的风险：
- 期望可逆的操作（如加密、版本控制中的文件还原）如果不是双射的，就会导致“单向门”效应：一旦数据被处理，就无法还原。这在很多关键业务场景中是不可接受的。
内存与空间效率：
- 如果一个映射不是单射的，为了处理冲突（例如哈希表的链表法），可能需要额外的内存空间。在处理大规模数据时，这会显著增加内存开销。
- 在一些数据结构中，如果不能保证双射，可能需要维护额外的索引或映射表来实现反向查找，这也会增加空间复杂度。