
(1)若二叉树为空,则为空操作,返回空。
(2)访问根结点。
(3)前序遍历左子树。
(4)前序遍历右子树。
a.二叉树前序遍历的递归算法:
void PreOrderTraverse(BiTree BT)
{ if(BT)
{
printf("%c",BT->data); //访问根结点
PreOrderTraverse(BT->lchild); //前序遍历左子树
PreOrderTraverse(BT->rchild); //前序遍历右子树 }
}b.使用栈存储每个结点右子树的二叉树前序遍历的非递归算法:
(1)当树为空时,将指针p指向根结点,p为当前结点指针。
(2)先访问当前结点p,并将p压入栈S中。
(3)令p指向其左孩子。
(4)重复执行步骤(2)、(3),直到p为空为止。
(5)从栈S中弹出栈顶元素,将p指向此元素的右孩子。
(6)重复执行步骤(2)~(5),直到p为空并且栈S也为空。
(7)遍历结束。
使用栈的前序遍历的非递归算法:
void PreOrderNoRec(BiTree BT)
{
stack S;
BiTree p=BT->root; while((NULL!=p)||!StackEmpty(S))
{ if(NULL!=p)
{
printf("%c",p->data);
Push(S,p);
p=p->lchild;
} else
{
p=Top(S);
Pop(S);
p=p->rchild;
}
}
}c.使用二叉链表存储的二叉树前序遍历非递归算法:
void PreOrder(pBinTreeNode pbnode)
{
pBinTreeNode stack[100];
pBinTreeNode p; int top;
top=0;
p=pbnode; do
{ while(p!=NULL)
{
printf("%d\n",p->data); //访问结点p
top=top+1;
stack[top]=p;
p=p->llink; //继续搜索结点p的左子树 } if(top!=0)
{
p=stack[top];
top=top-1;
p=p->rlink; //继续搜索结点p的右子树 }
}while((top!=0)||(p!=NULL));
} void InOrderTraverse(BiTree BT)
{ if(BT)
{
InOrderTraverse(BT->lchild); //中序遍历左子树
printf("%c",BT->data); //访问根结点
InOrderTraverse(BT->rchild); //中序遍历右子树 }
}b.使用栈存储的二叉树中序遍历的非递归算法:
void IneOrderNoRec(BiTree BT)
{
stack S;
BiTree p=BT->root; while((NULL!=p)||!StackEmpty(S))
{ if(NULL!=p)
{
Push(S,p);
p=p->lchild;
} else
{
p=Top(S);
Pop(S);
printf("%c",p->data);
p=p->rchild;
}
}
}c.使用二叉链表存储的二叉树中序遍历非递归算法:
void InOrder(pBinTreeNode pbnode)
{
pBinTreeNode stack[100];
pBinTreeNode p; int top;
top=0;
p=pbnode; do
{ while(p!=NULL)
{
top=top+1;
stack[top]=p; //结点p进栈
p=p->llink; //继续搜索结点p的左子树 } if(top!=0)
{
p=stack[top]; //结点p出栈
top=top-1;
printf("%d\n",p->data); //访问结点p
p=p->rlink; //继续搜索结点p的右子树 }
}while((top!=0)||(p!=NULL));
} void PostOrderTraverse(BiTree BT)
{ if(BT)
{
PostOrderTraverse(BT->lchild); //后序遍历左子树
PostOrderTraverse(BT->rchild); //后序遍历右子树
printf("%c",BT->data); //访问根结点 }
}b.使用栈存储的二叉树后序遍历的非递归算法:
算法思想:首先扫描根结点的所有左结点并入栈,然后出栈一个结点,扫描该结点的右结点并入栈,再扫描该右结点的所有左结点并入栈,当一个结点的左、右子树均被访问后再访问该结点。因为在递归算法中,左子树和右子树都进行了返回,因此为了区分这两种情况,还需要设置一个标识栈tag,当tag的栈顶元素为0时表示从左子树返回,为1表示从右子树返回。
(1)当树为空时,将指针p指向根结点,p为当前结点指针。
(2)将p压入栈S中,0压入栈tag中,并令p指向其左孩子。
(3)重复执行步骤(2),直到p为空。
(4)如果tag栈中的栈顶元素为1,跳至步骤(6)。
(5)如果tag栈中的栈顶元素为0,跳至步骤(7)。
(6)将栈S的栈顶元素弹出,并访问此结点,跳至步骤(8)。
(7)将p指向栈S的栈顶元素的右孩子。
(8)重复执行步骤(2)~(7),直到p为空并且栈S也为空。
(9)遍历结束。
使用栈的后序遍历非递归算法:
void PostOrderNoRec(BiTree BT)
{
stack S;
stack tag;
BiTree p=BT->root; while((NULL!=p)||!StackEmpty(S))
{ while(NULL!=p)
{
Push(S,p);
Push(tag,0);
p=p->lchild;
} if(!StackEmpty(S))
{ if(Pop(tag)==1)
{
p=Top(S);
Pop(S);
printf("%c",p->data);
Pop(tag); //栈tag要与栈S同步 } else
{
p=Top(S); if(!StackEmpty(S))
{
p=p->rchild;
Pop(tag);
Push(tag,1);
}
}
}
}
}c.使用二叉链表存储的二叉树后序遍历非递归算法:
void PosOrder(pBinTreeNode pbnode)
{
pBinTreeNode stack[100]; //结点的指针栈 int count[100]; //记录结点进栈次数的数组 pBinTreeNode p; int top;
top=0;
p=pbnode; do
{ while(p!=NULL)
{
top=top+1;
stack[top]=p; //结点p首次进栈
count[top]=0;
p=p->llink; //继续搜索结点p的左子树 }
p=stack[top]; //结点p出栈
top=top-1; if(count[top+1]==0)
{
top=top+1;
stack[top]=p; //结点p首次进栈
count[top]=1;
p=p->rlink; //继续搜索结点p的右子树 } else
{
printf("%d\n",p->data); //访问结点p
p=NULL;
}
}while((top>0));
}
typedef struct node
{
DataType data; struct node *lchild, *rchild; //左、右孩子指针 int ltag, rtag; //左、右线索
}TBinTNode; //结点类型
typedef TBinTNode *TBinTree;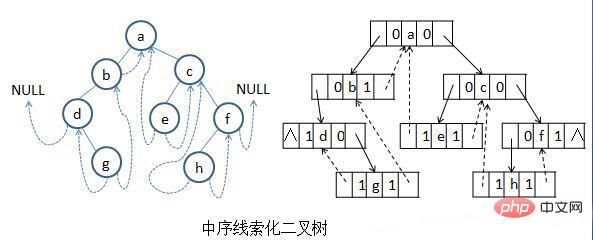
(1)中序线索化二叉树的算法:
void InOrderThreading(TBinTree p)
{ if(p)
{
InOrderThreading(p->lchild); //左子树线索化 if(p->lchild)
p->ltag=0; else
p->ltag=1; if(p->rchild)
p->rtag=0; else
p->rtag=1; if(*(pre)) //若*p的前驱*pre存在 { if(pre->rtag==1)
pre->rchild=p; if(p->ltag==1)
p->lchild=pre;
}
pre=p; //另pre是下一访问结点的中序前驱
InOrderThreading(p->rchild); //右子树线索化 }
}(2)在中序线索化二叉树下,结点p的后继结点有以下两种情况:
①结点p的右子树为空,那么p的右孩子指针域为右线索,直接指向结点p的后继结点。 TBinTNode *InOrderSuc(BiThrTree p)
{
TBinTNode *q; if(p->rtag==1) //第①情况 return p->rchild; else //第②情况 {
q=p->rchild; while(q->ltag==0)
q=q->lchild; return q;
}
}中序线索化二叉树求前驱结点的算法:
TBinTNode *InOrderPre(BiThrTree p)
{
TBinTNode *q; if(p->ltag==1) return p->lchild; else
{
q=p->lchild; //从*p的左孩子开始查找 while(q->rtag==0)
q=q->rchild; return q;
}
}(3)遍历中序线索化二叉树的算法
void TraversInOrderThrTree(BiThrTree p)
{ if(p)
{ while(p->ltag==0)
p=p->lchild; while(p)
{
printf("%c",p->data);
p=InOrderSuc(p);
}
}
}更多常见问题的相关技术文章,请访问常见问题栏目进行学习!
以上就是二叉树的遍历算法的详细内容,更多请关注php中文网其它相关文章!

每个人都需要一台速度更快、更稳定的 PC。随着时间的推移,垃圾文件、旧注册表数据和不必要的后台进程会占用资源并降低性能。幸运的是,许多工具可以让 Windows 保持平稳运行。

Copyright 2014-2025 https://www.php.cn/ All Rights Reserved | php.cn | 湘ICP备2023035733号