这里我们将看到如何计算三维空间中两个平面之间的角度。平面是 p1 和 p2。 pi 的方程如下 -
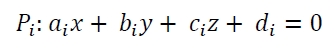
如果角度为“A”,则遵循此规则 -
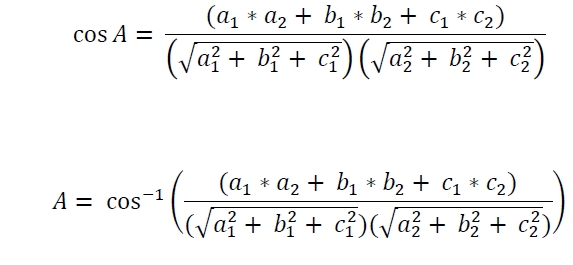
#include <iostream>
#include <cmath>
using namespace std;
class Plane{
private:
double a, b, c, d;
public:
Plane(double a = 0, double b = 0, double c = 0, double d = 0){
this->a = a;
this->b = b;
this->c = c;
this->d = d;
}
double friend angle(Plane p1, Plane p2);
};
double angle(Plane p1, Plane p2){
double nume = (p1.a * p2.a) + (p1.b * p2.b) + (p1.c * p2.c);
double deno1 = (p1.a * p1.a) + (p1.b * p1.b) + (p1.c * p1.c);
double deno2 = (p2.a * p2.a) + (p2.b * p2.b) + (p2.c * p2.c);
return (180.0 / 3.14159) * acos(nume/ (sqrt(deno1) * sqrt(deno2)));
}
int main() {
Plane p1(2.0, 2.0, -3.0, -5.0), p2(3.0, -3.0, 5.0, -6.0);
cout << "Angle: " << angle(p1, p2) << " degree";
}Angle: 123.697 degree
以上就是在C程序中,将以下内容翻译为中文:3D中两个平面的夹角的详细内容,更多请关注php中文网其它相关文章!

每个人都需要一台速度更快、更稳定的 PC。随着时间的推移,垃圾文件、旧注册表数据和不必要的后台进程会占用资源并降低性能。幸运的是,许多工具可以让 Windows 保持平稳运行。




Copyright 2014-2025 https://www.php.cn/ All Rights Reserved | php.cn | 湘ICP备2023035733号