盘点图像分割中的损失函数

1. 概要

损失函数主要是用于评估模型的预测值和真实标签的匹配程度的重要指标。基于图像分割的损失函数可大致分为4类。

1.1 损失函数

损失函数主要是用于评估模型的预测值和真实标签的匹配程度的重要指标。一般形式上，损失函数 L 采用期望风险最小化的形式表示：

$$L=E(G,S)$$L=E(G,S)

其中， $G=g_i,S=s_i$G=gi,S=si 分别表示真实标签和预测的分割图像。

1.2 汇总

16种基于图像分割的损失函数可大致分为4类

• 基于分布的损失函数 （Distribution-based）
• 基于区域的损失函数 （Region-based）
• 基于边界的损失函数 （Boundary-based)
• 基于复合的损失函数 （Compounded）

2. Distribution-based loss

基于分布的损失函数

2.1 Binary Cross-Entropy：

二分类交叉熵损失函数

交叉熵定义为对给定随机变量或事件集的两个概率分布之间的差异的度量。它被广泛用于分类任务，并且由于分割是像素级分类，因此效果很好。

在多分类任务中， 经常采用 softmax 激活函数+交叉熵损失函数，因为交叉熵描述了两个概率分布的差异，然而神经网络输出的是向量，并不是概率分布的形式。所以需要 softmax激活函数将一个向量进行“归一化”成概率分布的形式，再采用交叉熵损失函数计算 loss。

表达式：

图像转图像AI

利用AI轻松变形、风格化和重绘任何图像

65

查看详情

$$L=-[y\log \widehat{y}+(1-y)\log (1-\widehat{y})]$$L=−[ylogy^+(1−y)log(1−y^)]

$y_i$yi 表示样本i的label，正类为1，负类为0。

$P(y=1\mathrm{\mid }x)=\widehat{y}$P(y=1∣x)=y^表示预测值.

计算 N 个样本的总的损失函数:

$$L=-\sum _{i=1}^N[y_i\log {\widehat{y}}_i+(1-y_i)\log (1-{\widehat{y}}_i)]$$L=−i=1∑N[yilogy^i+(1−yi)log(1−y^i)]

#paddle已实现import paddlefrom paddle.nn import loss

loss.BCELoss() # 二分类loss.CrossEntropyLoss() # 多分类交叉熵

缺点：

当图像分割任务只需要分割前景和背景两种情况。当前景像素的数量远远小于背景像素的数量时，即$y=0$y=0的数量远大于$y=1$y=1的数量，损失函数中$y=0$y=0的成分就会占据主导，使得模型严重偏向背景，导致效果不好。

2.2 Weighted Binary Cross-Entropy

加权交叉熵损失函数

加权交叉熵损失函数只是在交叉熵Loss的基础上为每一个类别添加了一个权重参数为正样本加权。设置$\beta >1$β>1，减少假阴性；设置$\beta <1$β<1，减少假阳性。这样相比于原始的交叉熵Loss，在样本数量不均衡的情况下可以获得更好的效果。

表达式：

$$WCE(p,\widehat{p})=-[\beta p\log \widehat{p}+(1-p)\log (1-\widehat{p})]$$WCE(p,p)=−[βplogp+(1−p)log(1−p)]

#paddle已实现import paddlefrom paddle.nn import lossloss.CrossEntropyLoss(weight=weight)

缺点:

需要人为的调整困难样本的权重，增加调参难度

2.3 Balanced Cross-Entropy

平衡交叉熵损失函数

与加权交叉熵损失函数类似，但平衡交叉熵损失函数对负样本也进行加权。

表达式：

$$BCE(p,\widehat{p})=-[\beta p\log \widehat{p}+(1-\beta )(1-p)\log (1-\widehat{p})]$$BCE(p,p^)=−[βplogp^+(1−β)(1−p)log(1−p^)]

2.4 Focal Loss

Focal loss是在目标检测领域提出来的。其目的是关注难例（也就是给难分类的样本较大的权重）。对于正样本，使预测概率大的样本（简单样本）得到的loss变小，而预测概率小的样本（难例）loss变得大，从而加强对难例的关注度。

表达式：

$$FL(p,\widehat{p})=-[\alpha (1-\widehat{p}{)}^{\gamma }p\log \widehat{p}+(1-\alpha ){\widehat{p}}^{\gamma }(1-p)\log (1-\widehat{p})]$$FL(p,p^)=−[α(1−p^)γplogp^+(1−α)p^γ(1−p)log(1−p^)]

#paddle已实现import paddlefrom paddle.nn import functional as FF.sigmoid_focal_loss()

缺点：

引入了额外参数，增加了调参难度，目前在图像分割上只是适应于二分类。

2.5 Distance map derived loss penalty term

距离图得出的损失惩罚项

可以将距离图定义为ground truth与预测图之间的距离（欧几里得距离、绝对距离等）。合并映射的方法有2种，一种是创建神经网络架构，在该算法中有一个用于分割的重建head，或者将其引入损失函数。遵循相同的理论，可以从GT mask得出的距离图，并创建了一个基于惩罚的自定义损失函数。使用这种方法，可以很容易地将网络引导到难以分割的边界区域。

paper: https://arxiv.org/pdf/1908.03679.pdf

表达式：

$$L(y,p)=\frac{1}{N}\sum _{i=1}^N(1+\varphi )(\mathrm{\Theta })L_{CE}(y,p)$$L(y,p)=N1i=1∑N(1+ϕ)(Θ)LCE(y,p)

3. Region-based loss

基于区域的损失函数

3.1 Dice Loss

Dice系数是计算机视觉界广泛使用的度量标准，用于计算两个图像之间的相似度。在2016年的时候，它也被改编为损失函数，称为Dice损失。

Dice系数： 是用来度量集合相似度的度量函数，通常用于计算两个样本之间的像素之间的相似度，

公式如下：

$$s=\frac{2\mathrm{\mid }X\cap Y\mathrm{\mid }}{\mathrm{\mid }X\mathrm{\mid }+\mathrm{\mid }Y\mathrm{\mid }}=\frac{2TP}{2TP+FN+FP}$$s=∣X∣+∣Y∣2∣X∩Y∣=2TP+FN+FP2TP

分子中之所以有一个系数2是因为分母中有重复计算X和Y的原因，s的取值范围是[0,1]。而针对分割任务来说，X表示的就是Ground Truth分割图像，而Y代表的就是预测的分割图像。

表达式：

$$s=1-\frac{2\mathrm{\mid }X\cap Y\mathrm{\mid }}{\mathrm{\mid }X\mathrm{\mid }+\mathrm{\mid }Y\mathrm{\mid }}$$s=1−∣X∣+∣Y∣2∣X∩Y∣

此处，在分子和分母中添加1以确保函数在诸如y = 0的极端情况下的确定性。Dice Loss使用与样本极度不均衡的情况，如果一般情况下使用Dice Loss会回反向传播有不利的影响，使得训练不稳定。

#paddle已实现import paddlefrom paddle.nn import functional as FF.dice_loss()

缺点：

对小目标十分不利，因为在只有前景和背景的情况下，小目标一旦有部分像素预测错误，那么就会导致Dice大幅度的变动，从而导致梯度变化剧烈，训练不稳定。

3.2 Generalized Dice loss

当病灶分割有多个区域时，一般针对每一类都会有一个DICE，而Generalized Dice index将多个类别的dice进行整合，使用一个指标对分割结果进行量化。

paper：https://arxiv.org/pdf/1707.03237.pdf

表达式：

$$GDL=1-2\frac{\sum _{l=1}^L{w}_l\sum _n{r}_{ln}{p}_{ln}}{\sum _{l=1}^L{w}_l\sum _n{r}_{ln}{p}_{ln}+p_{ln}}$$GDL=1−2∑l=1Lwl∑nrlnpln+pln∑l=1Lwl∑nrlnpln

$w_l$wl为每个类别的权重， $r_{ln}$rln为类别$l$l在第$n$n个像素的标准值（GT），而$p_{ln}$pln为相应的预测概率值

$$w_l=\frac{1}{(\sum _{n=1}^N{r}_{ln}{)}^2}$$wl=(∑n=1Nrln)21

效果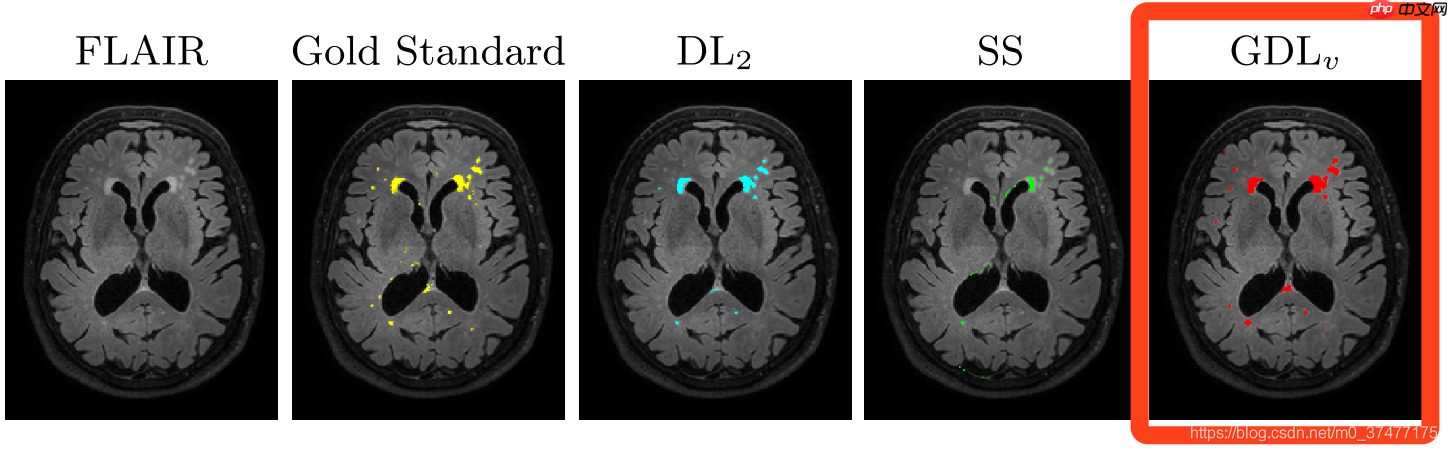         

缺点： 在AnatomyNet中提到GDL面对极度不均衡的情况下，训练的稳定性仍然不能保证

3.3 Tversky Loss

Tversky系数是Dice系数和 Jaccard 系数的一种推广。当设置α=β=0.5，此时Tversky系数就是Dice系数。而当设置α=β=1时，此时Tversky系数就是Jaccard系数。α和β分别控制假阴性和假阳性。通过调整α和β，可以控制假阳性和假阴性之间的平衡。

paper： https://arxiv.org/pdf/1706.05721.pdf

表达式：

$$T(A,B)=\frac{\mathrm{\mid }A\cap B\mathrm{\mid }}{\mathrm{\mid }A\cap B\mathrm{\mid }+\alpha \mathrm{\mid }A-B\mathrm{\mid }+\beta \mathrm{\mid }B-A\mathrm{\mid }}$$T(A,B)=∣A∩B∣+α∣A−B∣+β∣B−A∣∣A∩B∣

$$TL(p,\widehat{p})=1-\frac{1+p\widehat{p}}{1+p\widehat{p}+\beta (1-p)\widehat{p}+(1-\beta )p(1-\widehat{p})}$$TL(p,p)=1−1+pp+β(1−p)p+(1−β)p(1−p)1+pp

3.4 Focal Tversky Loss

与“Focal loss”相似，后者着重于通过降低易用/常见损失的权重来说明困难的例子。Focal Tversky Loss还尝试借助γ系数来学习诸如在ROI（感兴趣区域）较小的情况下的困难示例

paper： https://arxiv.org/pdf/1810.07842.pdf

表达式：

$$FTL=\sum _c(1-T{I}_c{)}^{\gamma }$$FTL=c∑(1−TIc)γ

3.5 Sensitivity Specificity Loss

敏感性–特异性 loss

sensitivity-specificity loss通过提高特异性的权重来解决类别不平衡的问题。

paper： http://www.rogertam.ca/Brosch_MICCAI_2015.pdf

1. 敏感性即召回率，检测出确实有病的能力：

$$Sensitivity=\frac{TP}{TP+FN}$$Sensitivity=TP+FNTP

2. 特异性，检测出确实没病的能力：

$$Specificity=\frac{TN}{TN+FP}$$Specificity=TN+FPTN

Sensitivity Specificity Loss:

$$SS=\lambda \frac{\sum _{n=1}^N(r_n-p_n{)}^2{r}_n}{\sum _{n=1}^N{r}_n+ϵ}+(1-\lambda )\frac{\sum _{n=1}^N(r_n-p_n{)}^2(1-r_n)}{\sum _{n=1}^N(1-r_n)+ϵ}$$SS=λ∑n=1Nrn+ϵ∑n=1N(rn−pn)2rn+(1−λ)∑n=1N(1−rn)+ϵ∑n=1N(rn−pn)2(1−rn)

其中式左边为病灶像素的错误率即$1\text{−}Sensitivity$1−Sensitivity ，而不是正确率，所以设置λ 为0.05。其中$(r_n-p_n{)}^2$(rn−pn)2是为了得到平滑的梯度。

3.6 Log-Cosh Dice Loss

Dice系数是一种用于评估分割输出的度量标准。它也已修改为损失函数，因为它可以实现分割目标的数学表示。同时，Log-Cosh方法已广泛用于基于回归的问题中，以平滑曲线。

paper： https://arxiv.org/pdf/2006.14822.pdf

示意图：         

将Cosh(x)函数和Log(x)函数合并，可以得到Log-Cosh Dice Loss：

$$L_{lc-dce}=\log (\mathrm{<a\; style="color:\#f60;\; text-decoration:underline;"\; title="cos"\; href="https://www.php.cn/zt/42725.html"\; target="\_blank">cos</a>h}(DiceLoss))$$Llc−dce=log(cosh(DiceLoss))

#paddle下实现import paddle
from paddle.nn import functional, loss

def lc_dce(pred, label):
    x = functional.dice_loss(pred, label)    return paddle.log(paddle.cosh(x))

缺点：

但是由于其非凸性，它多次都无法获得最佳结果。Lovsz-softmax损失旨在通过添加使用Lovsz扩展的平滑来解决非凸损失函数的问题。

3.7 Lovasz-Softmax Loss

LovaszSoftmax，是一种基于IOU的loss，效果优于cross_entropy，可以在分割任务中使用。

paper：https://arxiv.org/pdf/1705.08790.pdf

多分类任务中，把softmax + CE改造成基于IOU的loss, 主要过程如下：

softmax 函数：

$$f_i(c)=\frac{e^{F_i(c)}}{\sum _{c^{\mathrm{\prime }}}\in c{e}^{F_i(c^{\mathrm{\prime }})}},\mathrm{\forall }i\in [1,p],\mathrm{\forall }c\in C$$fi(c)=∑c′∈ceFi(c′)eFi(c),∀i∈[1,p],∀c∈C

CE:

$$loss(f)=-\frac{1}{p}\sum _{i=1}^p\log f_i(y_i^{\ast })$$loss(f)=−p1i=1∑plogfi(yi∗)

一个像素的类别：

$${\tilde{y}}_i=\underset{c\in C}{}{F}_i(c)$$y~i=c∈CargmaxFi(c)

表达式

$$J_c(y^{\ast },\tilde{y})=\frac{\mathrm{\mid }(y^{\ast }=c)\cap (\tilde{y}=c)\mathrm{\mid }}{\mathrm{\mid }(y^{\ast }=c)\cup (\tilde{y}=c)\mathrm{\mid }}$$Jc(y∗,y~)=∣(y∗=c)∪(y~=c)∣∣(y∗=c)∩(y~=c)∣

$$\mathrm{\Delta }{J}_c(y^{\ast },\tilde{y})=1-J_c(y^{\ast },\tilde{y})$$ΔJc(y∗,y~)=1−Jc(y∗,y~)

4. Boundary-based loss

基于边界的损失函数

4.1 Shape-aware Loss

Shape-aware Loss考虑了形状。通常，所有损失函数都在像素级起作用，Shape-aware Loss会计算平均点到曲线的欧几里得距离，即预测分割到ground truth的曲线周围点之间的欧式距离，并将其用作交叉熵损失函数的系数。

paper：https://arxiv.org/pdf/1908.03679.pdf

定义如下： （CE指交叉熵损失函数）

$$E_i=D(\widehat{C},C_{GT})$$Ei=D(C^,CGT)

$$L_{shape-aware}=-\sum _{i}CE(y,\widehat{y})-\sum _i{E}_{i}CE(y,\widehat{y})$$Lshape−aware=−i∑CE(y,y^)−i∑EiCE(y,y^)

4.2 Hausdorff Distance Loss

Hausdorff Distance Loss（HD）是分割方法用来跟踪模型性能的度量.

paper: https://arxiv.org/pdf/1904.10030v1.pdf

定义式：

$$d(X,Y)=ma{x}_{x\in X}mi{n}_{y\in Y}\mathrm{\mid }\mathrm{\mid }x-y\mathrm{\mid }{\mathrm{\mid }}_2$$d(X,Y)=maxx∈Xminy∈Y∣∣x−y∣∣2

缺点：

任何分割模型的目的都是为了最大化Hausdorff距离，但是由于其非凸性，因此并未广泛用作损失函数。有研究者提出了基于Hausdorff距离的损失函数的3个变量，它们都结合了度量用例，并确保损失函数易于处理。

5. Compounded loss

基于复合的损失函数

5.1 Exponential Logarithmic Loss

focal loss + Dice loss

对focal loss 和 Dice loss进行指数和对数转换进行组合，这样网络就可以被迫的关注预测不准的部分，以合并更精细的分割边界和准确的数据分布。

paper：https://arxiv.org/pdf/1809.00076.pdf

定义式：

$$L_{Exp}=w_{Dice}{L}_{Dice}+w_{cross}{L}_{cross}$$LExp=wDiceLDice+wcrossLcross

$$L_{Dice}=E(-\ln (DC{)}^{\gamma Dice})$$LDice=E(−ln(DC)γDice)

$$L_{cross}=E(w_l(-\ln (p_l{)}^{\gamma cross}))$$Lcross=E(wl(−ln(pl)γcross))

新增添了4个参数权重分别是$w_{Dice}$wDice,  $w_{Cross}$wCross, ${\gamma }_{Dice}$γDice, ${\gamma }_{Cross}$γCross，给调参带来不小的麻烦

5.2 Combo Loss

Dice Loss +Balanced CE

组合损失定义为Dice loss和修正的交叉熵的加权和。它试图利用Dice损失解决类不平衡问题的灵活性，同时使用交叉熵进行曲线平滑。

定义为： （DL指Dice Loss）

$$L_{m-bce}=-\frac{1}{N}\sum _{i=1}^N[\beta y_i\log \widehat{y_i}+(1-\beta )(1-y)\log (1-\widehat{y_i})]$$Lm−bce=−N1i=1∑N[βyilogyi^+(1−β)(1−y)log(1−yi^)]

$$CL(y,\widehat{y})=\alpha L_{m-bce}-(1-\alpha )DL(y,\widehat{y})$$CL(y,y^)=αLm−bce−(1−α)DL(y,y^)

6. 实验与结果

数据集： NBFS Skull Stripping Dataset

实验细节： 使用了简单的2D U-Net模型架构

对比结果：

7. 总结

在设计基于复杂图像分割的深度学习架构时，损失函数的选择对于任何架构学习正确的目标都是至关重要的。

以上是关于图像分割损失函数的汇总：

主要包括4类损失函数。