什么是堆排序？堆排序的实现步骤-js教程-PHP中文网

什么是堆排序？堆排序的实现步骤

星降

发布： 2025-08-19 12:06:01

原创

491人浏览过

堆是一种特殊的完全二叉树，其中每个节点均大于（最大堆）或小于（最小堆）其子节点，堆排序通过构建和调整堆实现排序，首先将数组转化为最大堆，然后依次将堆顶最大值与末尾元素交换并重新堆化，直至有序；其时间复杂度为O(n log n)，空间复杂度为O(1)，属于原地不稳定排序，适用于大规模数据和内存受限环境。

什么是堆排序？堆排序的实现步骤

堆排序是一种基于二叉堆数据结构的排序算法。它利用堆的性质（最大堆或最小堆）来进行排序，效率较高。

堆排序的核心在于构建堆和调整堆。

构建堆的过程，就是把一个无序数组转换成一个堆结构。调整堆则是指，在堆顶元素发生变化后，如何维护堆的性质，使其仍然保持堆的结构。

如何理解堆排序的“堆”？

堆，本质上是一种特殊的完全二叉树。想象一下，你面前有一棵树，每个节点都比它的子节点大（或者小）。这就是堆的核心概念。如果每个节点都比子节点大，我们称之为最大堆；反之，如果每个节点都比子节点小，则称为最小堆。

堆排序正是利用了这种特性。首先，我们将待排序的数组构建成一个堆。然后，将堆顶元素（最大堆中的最大值，或最小堆中的最小值）与数组末尾元素交换。接着，将堆的大小减一，并重新调整堆，使其满足堆的性质。重复这个过程，直到堆的大小为1，此时数组就完成了排序。

这种“先整体构建，再逐步调整”的思想，是堆排序的关键。

堆排序的详细实现步骤

构建堆（Build Heap）：
- 从最后一个非叶子节点开始（即数组长度/2 - 1），从后向前遍历数组。
- 对每个节点执行“堆化”（Heapify）操作。
堆化（Heapify）：
- 比较当前节点与其子节点的值。
- 如果当前节点小于（或大于，取决于最大堆或最小堆）其子节点中的较大（或较小）值，则交换它们。
- 交换后，递归地对被交换的子节点执行堆化操作，直到满足堆的性质。
排序：

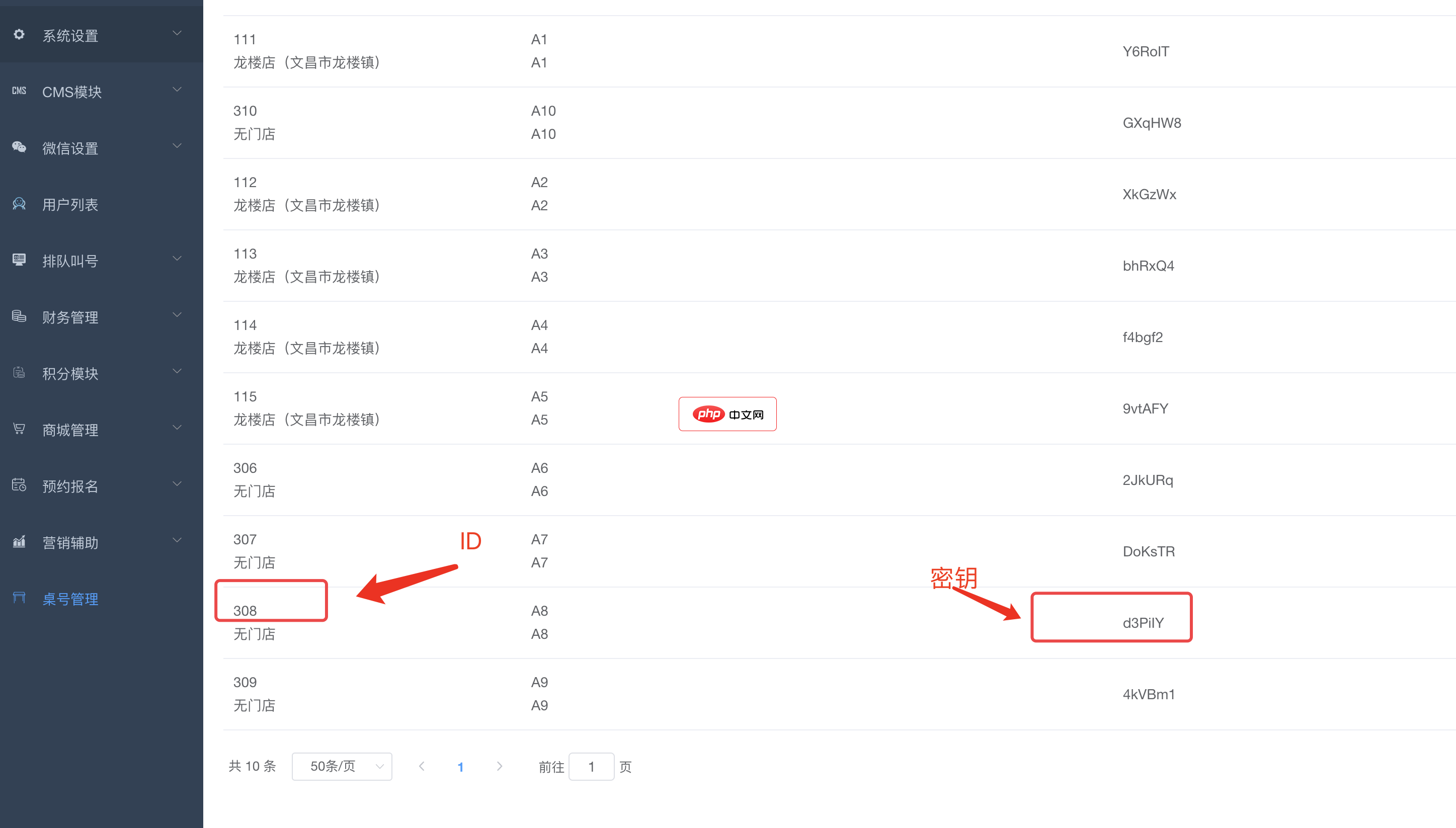
bee餐饮点餐外卖小程序
bee餐饮点餐外卖小程序是针对餐饮行业推出的一套完整的餐饮解决方案，实现了用户在线点餐下单、外卖、叫号排队、支付、配送等功能，完美的使餐饮行业更高效便捷！功能演示：1、桌号管理登录后台，左侧菜单 “桌号管理”，添加并管理你的桌号信息，添加以后在列表你将可以看到 ID 和密钥，这两个数据用来生成桌子的二维码2、生成桌子二维码例如上面的ID为 308，密钥为 d3PiIY，那么现在去左侧菜单微信设置

1

查看详情
- 将堆顶元素（最大值或最小值）与数组末尾元素交换。
- 将堆的大小减一。
- 对堆顶元素执行堆化操作，重新调整堆。
- 重复以上步骤，直到堆的大小为1。

下面是一个使用Python实现最大堆排序的代码示例：

def heapify(arr, n, i):
    largest = i  # 初始化最大值为根节点
    l = 2 * i + 1  # 左子节点
    r = 2 * i + 2  # 右子节点

    # 如果左子节点存在且大于根节点
    if l < n and arr[i] < arr[l]:
        largest = l

    # 如果右子节点存在且大于根节点和左子节点
    if r < n and arr[largest] < arr[r]:
        largest = r

    # 如果最大值不是根节点
    if largest != i:
        arr[i], arr[largest] = arr[largest], arr[i]  # 交换
        heapify(arr, n, largest)  # 递归地堆化子树


def heap_sort(arr):
    n = len(arr)

    # 构建最大堆
    for i in range(n // 2 - 1, -1, -1):
        heapify(arr, n, i)

    # 一个个从堆顶取出元素
    for i in range(n - 1, 0, -1):
        arr[i], arr[0] = arr[0], arr[i]  # 交换
        heapify(arr, i, 0)


# 示例
arr = [12, 11, 13, 5, 6, 7]
heap_sort(arr)
print("排序后的数组:", arr)

登录后复制

这段代码首先定义了