普利姆算法详解：轻松求解最小生成树

在日常生活中，最小生成树的应用十分普遍。例如，在连接n个城市时，只需建设n-1条线路即可实现连通，那么如何规划才能使总成本最低？可将每条线路的建设费用视为边的权值，把问题转化为求城市间连通图的最小生成树。此时，最小生成树所对应的连接方式，即为整体造价最低的方案，有效实现了资源优化与成本控制。

1、 最小生成树基础概念解析

2、 边上有权值的图称为带权图或网，其生成树也具有权重，生成树中所有边的权值之和即为该树的总权值。

3、 权值之和最小的生成树称为最小生成树。

4、 连接n个城市需n-1条线路，可将各线路成本视为边的权值。此时，最小生成树即为总造价最低的连通方案，广泛应用于网络、交通等规划领域。

5、 最小生成树具唯一最短连通性

6、 若连通图G＝(V,E)中，U为顶点集V的非空子集，且边(u,v)的权值最小，其中u属于U，v属于V减去U，则必可找到一棵最小生成树，该树包含边(u,v)。

7、 构建网络最小生成树需解决两个关键问题。

8、 优先选择权重较小的边，确保不形成环路。

9、 选择n-1条合适的边连接n个顶点。

10、 Prim算法核心：逐步扩展最小生成树。

11、 设G＝(V，E)为连通图，TE表示其最小生成树的边集。算法初始令U＝{u?}（u?∈V），TE为空集，随后不断迭代执行特定步骤。

12、 从所有连接U与V－U的边中选取权值最小的一条(u0,v0)，将其加入TE集合，并将v0加入U，重复此过程直至U包含V中所有顶点。

13、 此时TE包含n-1条边，T=(V,TE)构成G的最小生成树。

14、 Prim算法的关键在于每步添加的边都保持已选边集始终形成一棵生成树。

15、 读完上面大段文字是否感到困惑？接下来将通过分步图解，帮助大家更清晰地理解算法过程。

16、 先随便选个起点开始

17、 图中包含9个顶点，记为v1至v9，顶点集合为V={v1, v2, ..., v9}，各边均标有权值。执行Prim算法时，可任选一个顶点作为初始点，通常选择v1，起始点的选择不影响最终的最小生成树结果。设集合U表示当前已纳入最小生成树的顶点，集合TE用于存储已选中的边。算法逐步扩展U，每次选择连接U与外部顶点的最小权边，直至所有顶点都被包含，形成一棵完整的最小生成树。

18、 当前状态：顶点集U含v1，边集TE为空。

19、 第二步：基于上一步找出最小权值。

20、 在U={v1}与V-U两个顶点集之间，寻找连接它们且权值最小的边，即在图中红线交叉处找出权值最小的边。

21、 从图中可知，边v1-v8的权值最小，为2，因此将顶点v8并入集合U，并将边（v1，v8）添加至TE中。

22、 当前状态为：顶点集U包含v1和v8，边集TE仅含边(v1, v8)。

Text Mark

处理文本内容的AI助手

81

查看详情

23、 第三步：持续寻找权值最小的边

24、 在图中找出一个顶点属于集合U={v1，v8}，另一个顶点属于V-U的边中权值最小的一条，即在红线交叉处寻找最小权重。

25、 由图可知，边v8-v9的权值最小，为4，因此将顶点v9加入集合U，并将边(v8, v9)添加至TE中。

26、 当前状态为：顶点集U包含v1、v8、v9；边集TE包含(v1,v8)和(v8,v9)。

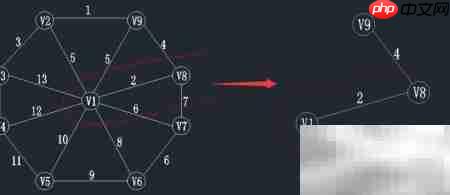
27、 第四步：基于上一步结果，持续寻找最小权重值。

28、 在图中找出一个顶点属于集合U={v1，v8，v9}，另一个顶点属于V-U的边中权值最小的一条，即在红线交叉处寻找最小权重。

29、 由图可知，边v9-v2的权重最小，为1，因此将顶点v2并入集合U，同时将边(v9, v2)加入边集TE中。

30、 当前状态为：U集合包含元素v1、v8、v9和v2。

31、 第五步：在前一步基础上，继续寻找最小权值。

32、 在U={v1，v8，v9，v2}与V-U的交界处，沿红线连接的边中，寻找权值最小的边。

33、 从图中可知，边v2-v3的权值最小，为3，因此将顶点v3加入集合U，并将边(v2, v3)添加至TE中。

34、 当前状态为：U 包含顶点 v1、v8、v9、v2 和 v3。

35、 第五至九步：在前一步基础上持续寻找最小权值。

36、 不断重复此过程，直至所有顶点都被找到。至此，相信大家已了解普利姆算法求最小生成树的步骤，但需特别注意以下三点。

37、 每次选择权重最小的边，若该边与已选边形成环路则舍弃，例中（v1，v9）、（v1，v2）等会导致环路的边不予采用。

38、 当遇到权值相同且均不会形成回路的边时，任选其一都不会影响最终生成树的结果。例中边（v3，v4）与（v6，v5）的权值均为9，无论优先选择哪一条，所得到的最小生成树结果都相同。

39、 选择n-1条合适边连接n个顶点。

40、 算法完整步骤详见图示。

41、 最小生成树是图中连接所有顶点且总权值最小的无环子图。

42、 Prim算法是求解最小生成树的方法之一，此外还有Kruskal等其他算法可供选择。

43、 时间复杂度为O(n?)，与边数无关，适用于稠密图的prim算法。

以上就是普利姆算法详解：轻松求解最小生成树的详细内容，更多请关注php中文网其它相关文章！